💡Introduction to Transformer

Transformer is a really popular method in modern neural networks. We have BERT or GPT to process the natural language and ViT to deal with computer vision. In this essay, you will understand what is the transformer and why the transformer works. But be careful, limited by my knowledge, I can’t show some mathematical theories or code of transformer for you.

Why do we need the Transformer?

In the NLP( Natural Language Processing) field, the text dataset always has some obvious features that prevent us from using MLP.

1. Too large after being encoder.

   To represent the words, we should embed them into vectors first. Generally, we use the vector of length 1024 to describe one word, meaning the data size will become large after multiplying the size of the vector(1024).

2. Having different length

   Our inputs for the NLP problems have various lengths according to the size of passages or sentences. We should build models that adopt different size inputs.

3. Ambiguous

   The texts don’t resemble the numbers having certain meanings from themselves. Some words like “it” refer to others in the context, which means they are ambiguous in different backgrounds.

To sum up, the features or problems we mention above prevent us from using normal structures like MLP to process natural language. So we need new things - Transformer. Let us approach this by self-attention first.

Self-attention

Parameter sharing

A standard neural network layer $f[x]$, take $D\times 1$ inputs and return $D'\times 1$. When we process embedding text, our input’s dimensions are changed to $D\times N$. To hold enough information in our model, we assume the size of our data remains unchanged, which means the size of outputs is also $D\times N$. Where $D$ is the size of the embedding vector, $N$ is the number of the word.

$$ v=\beta_v+\Omega_vx $$

Where $x$ is embedding word, $v$ is abstract meaning of word(present by number), and $\beta_v,\Omega_v$ is the parameter mapping the words to their meanings.

As we can use one dictionary to map every word to their meanings, we can just use $\beta_v,\Omega_v$ to map every embedding word, called parameter sharing

$$ V[X]=\beta_v1^T+\Omega_vX $$

From weight to self-attention

$$ O[X]=V[X]\times W $$$$ W=\begin{pmatrix} w_1 &\dots &w_n \\ \vdots & &\vdots \\ w_1 & \dots &w_n \end{pmatrix} $$$$ \begin{split} Q[X]=\beta_q1^T+\Omega_qX\\ K[X]=\beta_k1^T+\Omega_kX \end{split} $$

Where $\beta_q,\Omega_q,\beta_k,\Omega_q$ are also shared for every word.

$$ Sa[X]=V[X]\cdot \text{Softmax}[K[X]^TQ[X]] $$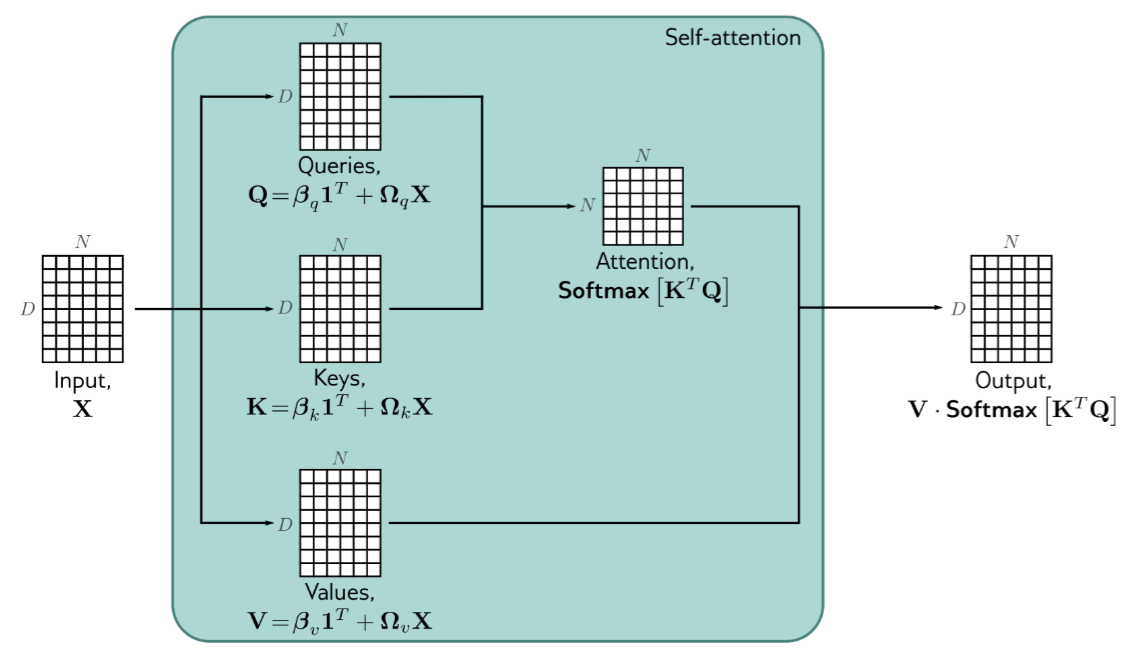

Typically, the dot products will be really large, which means the small changes to the inputs have nearly no effect on the output because we use the softmax function. So we always use the dimension of the input, always the shape of embedding, to scale the dot products.

$$ Sa[X]=V[X]\cdot \text{Softmax}[\frac{K[X]^TQ[X]}{\sqrt{D_q}}] $$

Multiple heads

$$ \text{MhSa}[X]=\Omega_c[Sa_1[X]^T,Sa_2[X]^T,\dots,Sa_H[X]^T]^T $$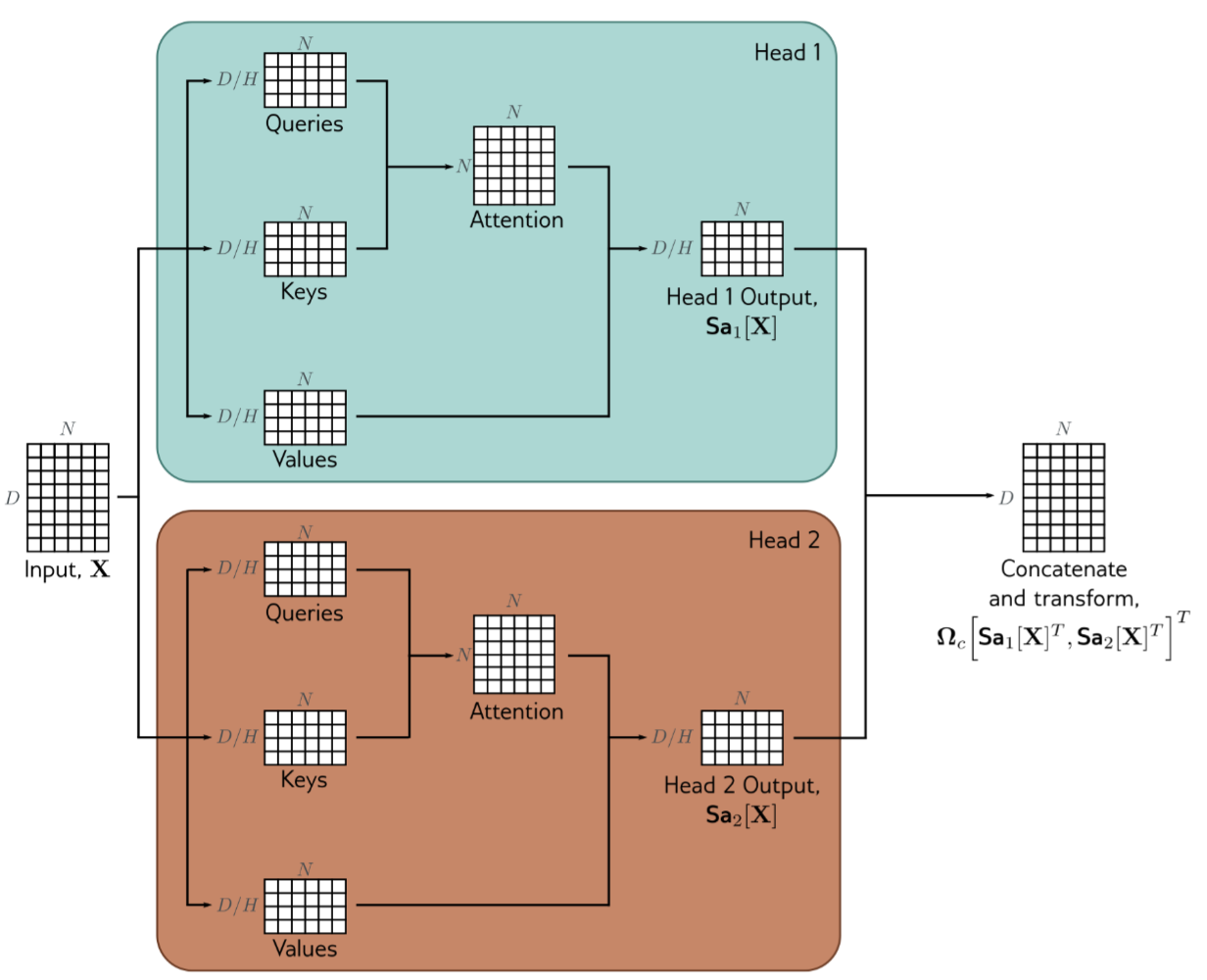

Transformer layers

$$ \begin{split} X \leftarrow X+\text{MhSa}[X]\\ X\leftarrow \text{LayerNorm}[X]\\ x_n\leftarrow x_n+\text{MLP}[x_n]\\ X\leftarrow \text{LayerNorm}[X] \end{split} $$

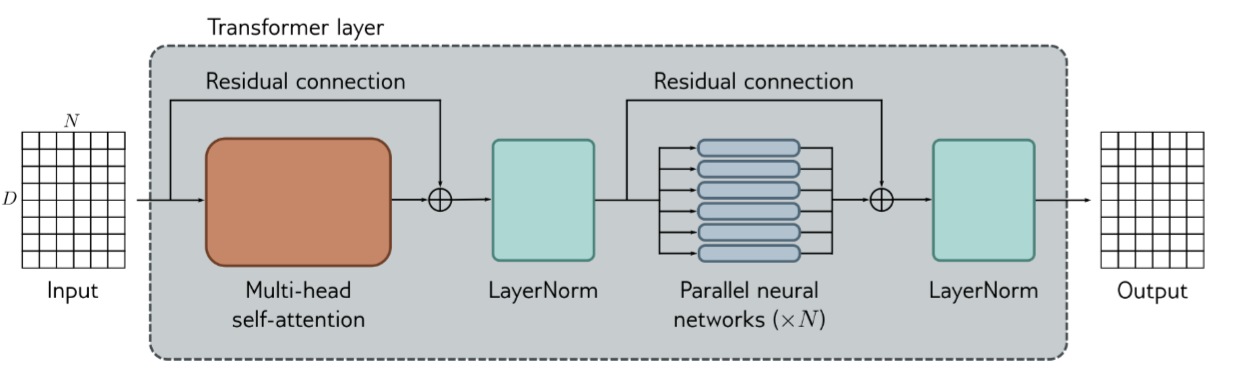
Where $\text{MLP}$ is fully connected network works separately on each word and $\text{LayerNorm}$ is the normalization happens in the channel, like:

$$ y=\frac{x-E[x]}{\sqrt{Var[x]+\epsilon }}*\gamma+\beta $$

Reference

[1] S. J. D. Prince, Understanding Deep Learning. MIT Press, 2023.

[2] A. Vaswani et al., ‘Attention Is All You Need’, CoRR, vol. abs/1706.03762, 2017.

All photos in this article are from Understanding Deep Learning. It’s a great book and I really recommend it