📑Reading Notes for "LTSF-Linear"

Overview

This paper insists that the time series is an ordered set of continuous points that will result in the loss of temporal information when using the Transformer structure. To prove this opinion, they propose models named LSTF-Linear which achieve outstanding performance and conduct comprehensive studies.

1. What problem does the paper try to solve？

   Attempt to verify whether the Transformer is effective in time series prediction problems and whether a simple model can surpass all current Transformer-based models.

2. What is the proposed solution?

   The LSTF Linear model was proposed as an alternative, achieving extremely high performance with only a single-layer network

3. What are the key experimental results in this paper?

   Achieved better performances than Transformer-based methods on multiple datasets such as electricity, healthcare, and meteorology

4. What are the main contributions of the paper?

   • Challenge the Transformer structure in the long-term time series forecasting task.
   • Introduce the LTSF-Linear model which only has one layer while achieving compared results in various fields.
   • Conduct comprehensive empirical studies on various aspects of existing Transformer-based solutions.

5. What are the strong points and weak points in this paper?

   • Strong Points： Proposed potential issues in the current research route and opened up a new perspective in a simple way.
   • Weak Points: Only conducted research on prediction problems and have not explored other issues, such as anomaly detection.

Background

Over the past several decades, the Transformer has been widely used as the TSF solution. However, the self-attention mechanism is permutation-invariant and anti-order which will cause the loss of temporal information. Typically, time series contain less semantic meaning compared with NLP or CV problems and need more temporal information, which will emphasize this problem. Thus, this paper tries to challenge the Transformer-based LSTF solution with direct multi-step forecasting strategies.

For the time series containing $C$ variates, the historical data can be represented as $\mathcal{X}=\{X_1^t,\dots,X_C^t\}_{t=1}^L$, wherein $L$ is the look-back window size. The forecasting problems need to predict $T$ feature time step’s value $\hat{\mathcal{X}}=\{\hat{X}_1^t,\dots,\hat{X}_C^t\}_{t=1}^L$. When $T>1$, the methods can be divided into two parts:

• Integrated multi-step(IMS): Learn a single-step forecaster and interactively apply it to obtain multi-step predictions. This method has a smaller variance but will cause error accumulation.
• Direct multi-step(DMS): Directly optimize the multi-step forecasting objective at one. This method can have more accurate predictions when $T$ is large.

Methods

Transformer-Based Methods

The vanilla Transformer model has some limitations when applied to time series problems, thus various works try to improve the performance by adding or replacing some parts of the Transformer. Generally speaking, it can be divided into four major parts.

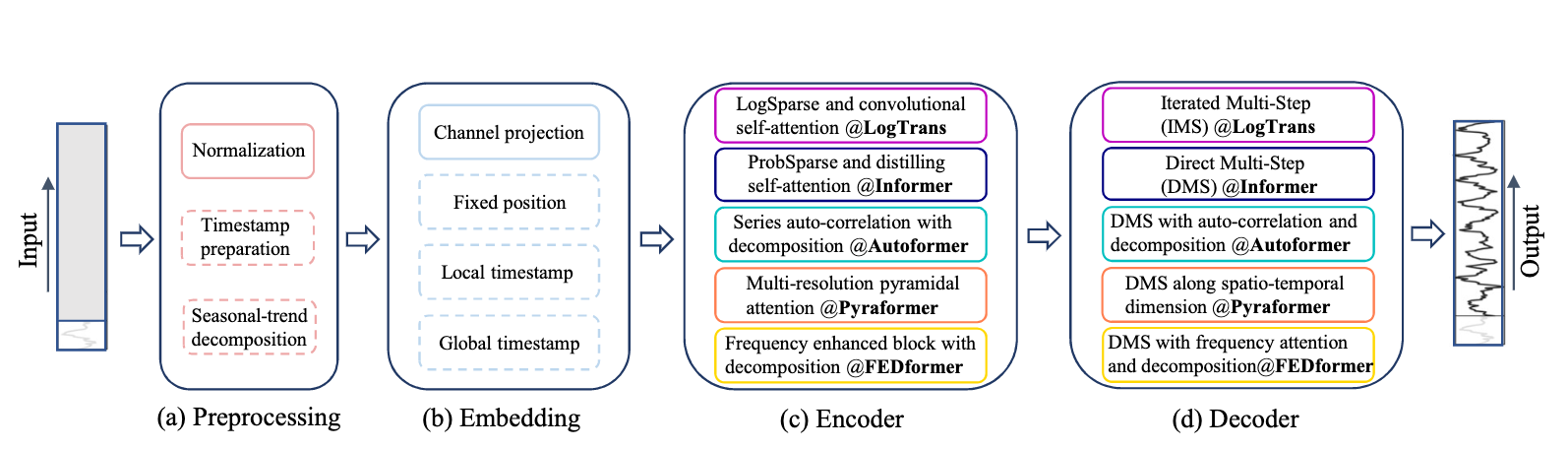
Preprocessing: To use Transformer to deal with time series datasets, some preprocessing is needed to adopt the data structures, such as normalization with zero-mean and adding timestamps as NLP did. Specifically, in Autoformer, seasonal-trend decomposition is proposed to get the trend part and the cyclical part, which helps data more clearly.

Embedding: In NLP’s Transformer, embedding will map the words to the vector in a typical space that reveals the meaning. In time series, time information is significantly important. Thus, various timestamp methods are proposed to help the model reserve the temporal information.

Encoder/Decoder: To help the Transformer structure adopt the time series problems, there have been many improvements made to the encoder and decoder in this work. Among them, in the encoder section, many improvements have been proposed to reduce computational consumption and increase speed. In the decoder section, to avoid cumulative errors, it has also begun to transition from IMS to DMS.

The success of Transformer in the NLP field is largely attributed to its understanding of the semantic relationships between words, but in time series problems, temporary information has become even more important. However, the Transformer’s ability to model time largely comes from the timestamp rather than its structure.

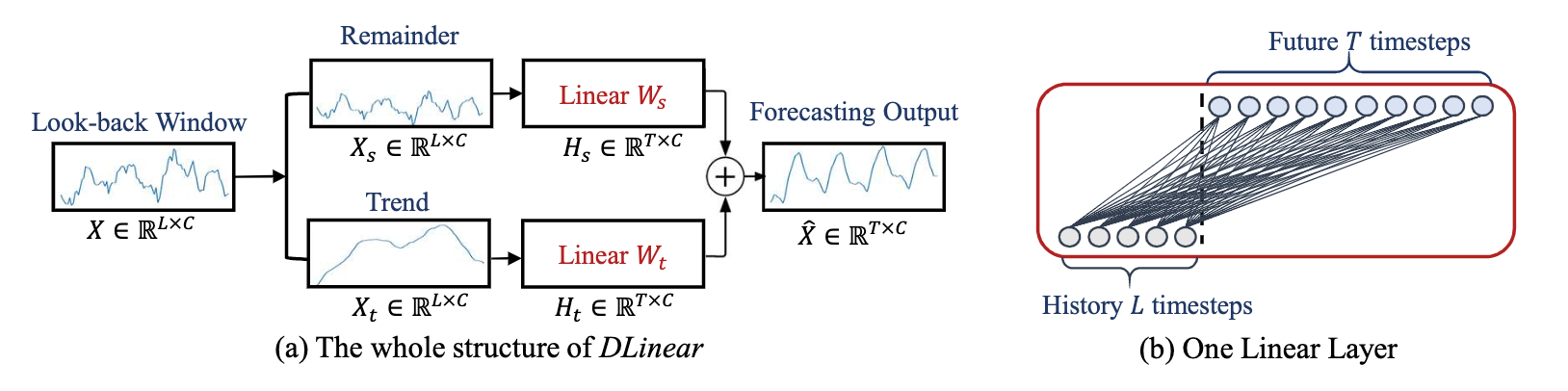
LSTF-Linear

This paper hypothesizes that the improvement in the Transformer-Based model is due to the DMS strategy rather than the Transformer. Thus they propose LSTF-Linear that directly regresses historical time series for future prediction via a weighted sum operation to verify this thinking. The model can be a formula as :

Wherein $W\in\mathbb{R}^{T\times L}$ is a linear layer along the temporal axis. Furthermore, this paper proposes two sub-models, DLinear which uses decomposition to obtain the trend part and the seasonal part, and the NLinear which subtracts a portion before making the prediction and rejoined it after making the prediction.

Experiments

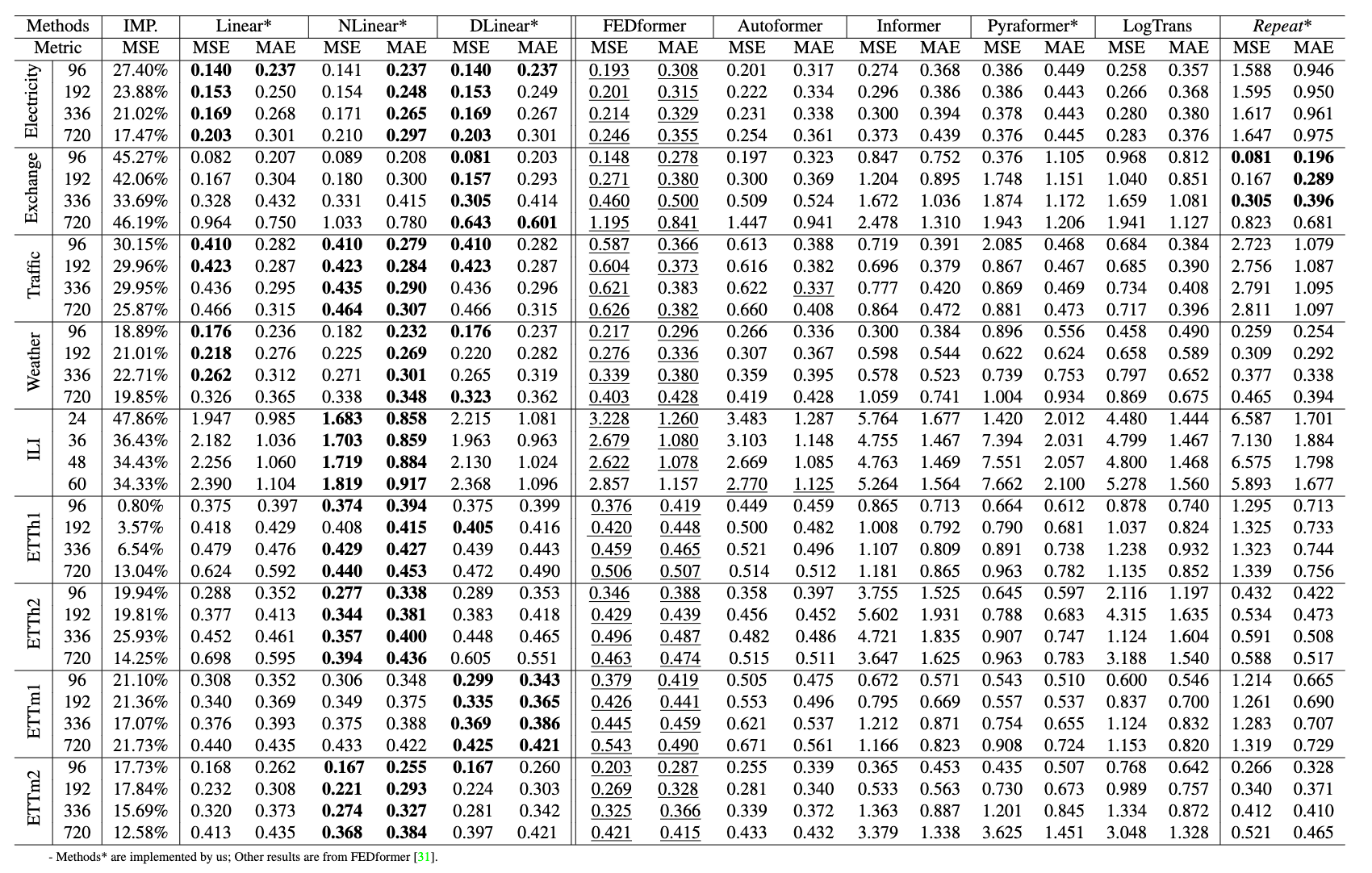
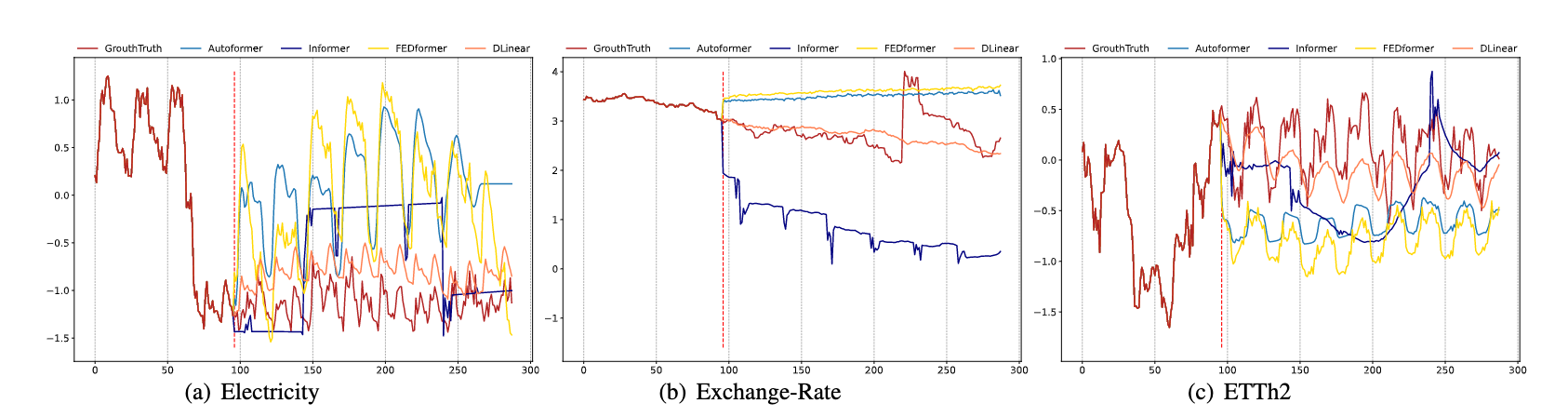
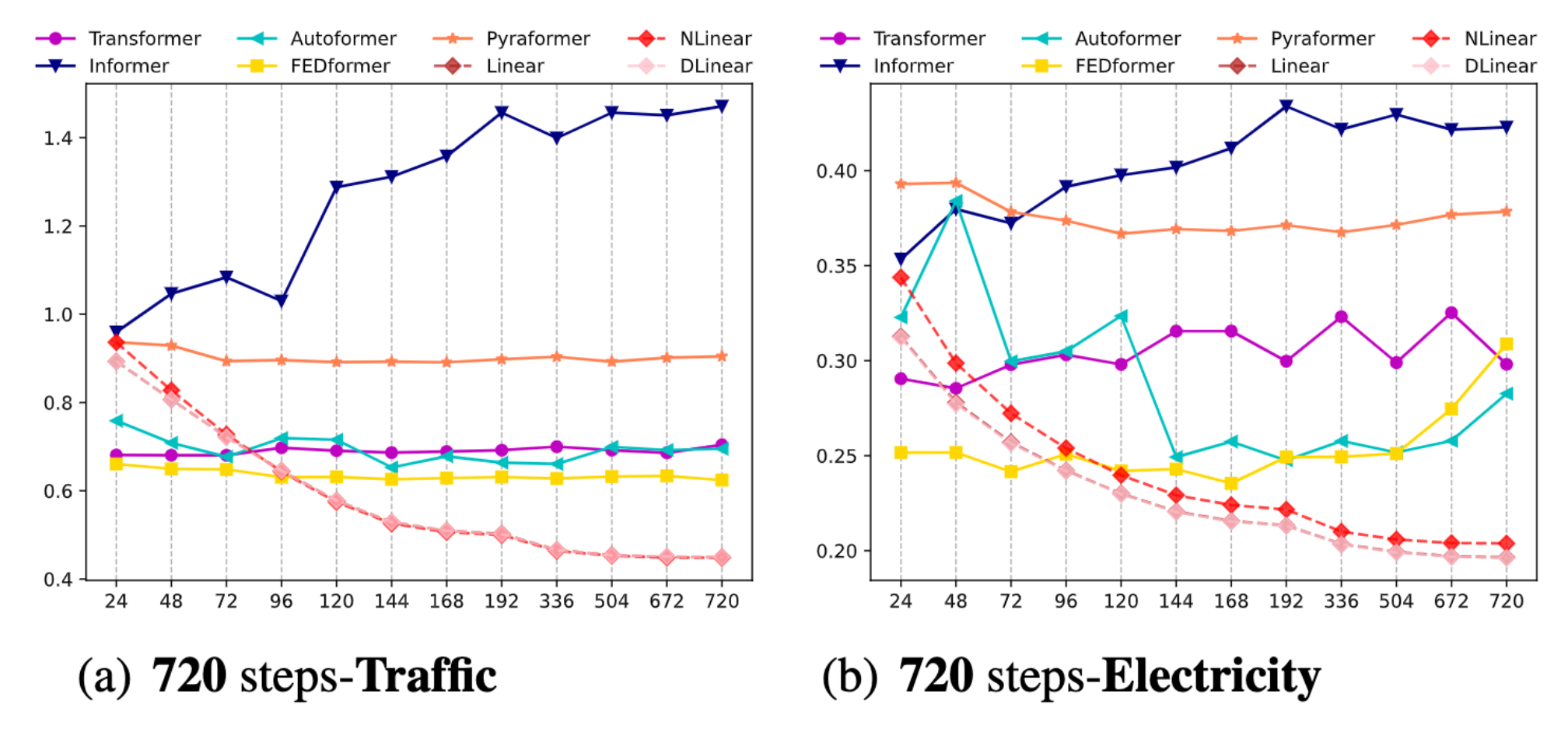
In order to verify the quality of the LSTF-Linear, the author selected some common sequence data from real life and compared with five popular Transformer-based model. All results are show as follow: